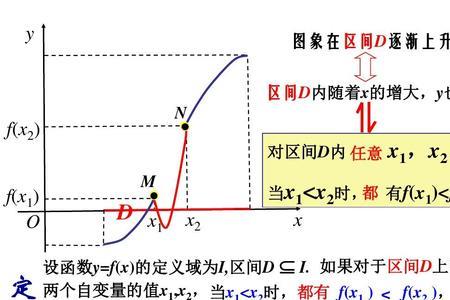
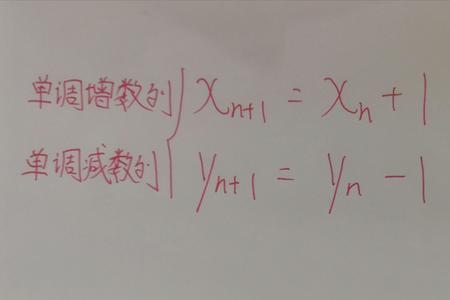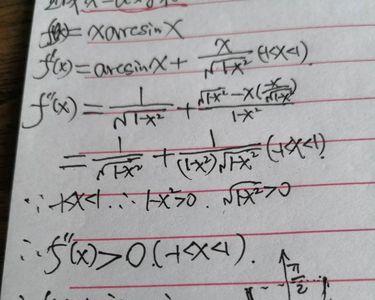函数的导数本质上是这个函数在某时刻的变化率,如果函数是单调不增的,那么在区间I上,若x1<x2,一定有f(x1)≥f(x2),所以当x2→x1时,lim(f(x2)-f(x1))/(x2-x1)必小于等于零,即函数的导数小于等于零,由此可知,单调不增函数的一阶导数大于0是错误的,它的一阶导数必小于等于0
单调不增函数的一阶导数大于0吗
有两种递增函数:
第一种:
严格单调递增:即y = e^x
它的导数是永远大于0的
第二种:
有些函数会存在拐点
例如y = x^3
虽然它是递增函数,但是在x = 0处的导数是0,这是拐点
所以并不是严格递增函数