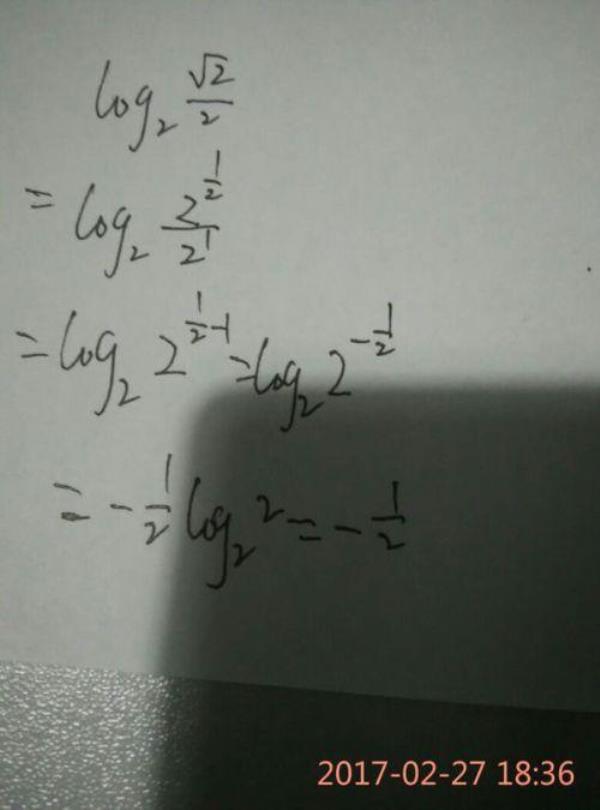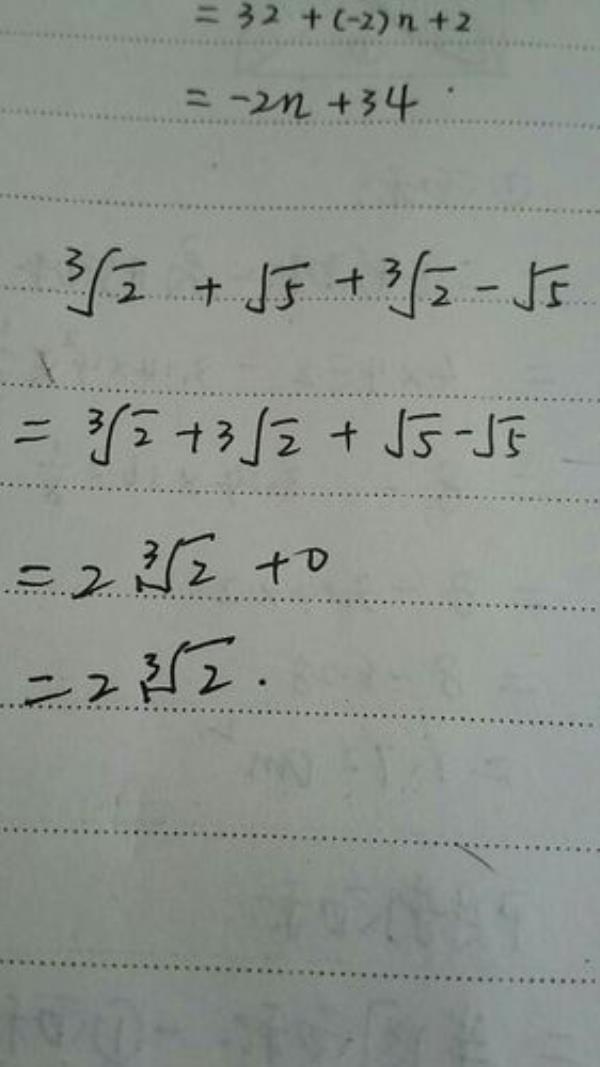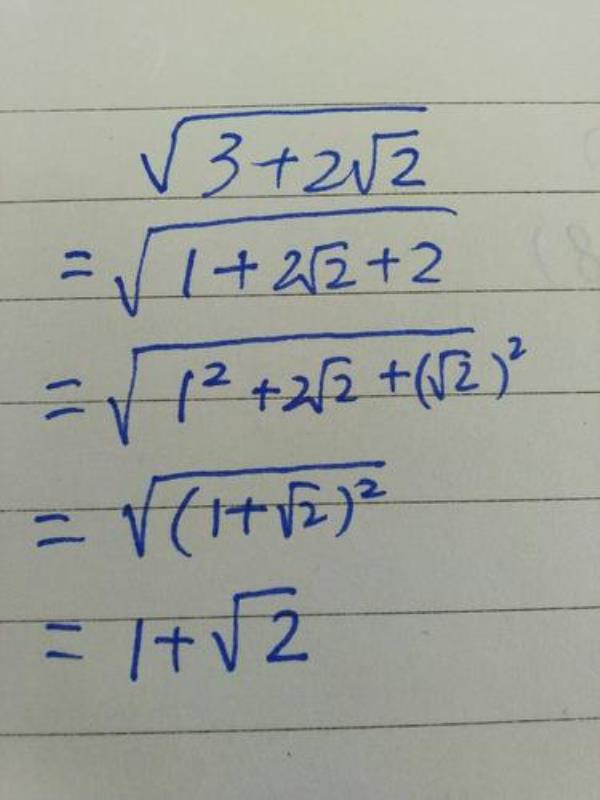根号下函数用泰勒公式的方法:
根号式子看成(1+(sinx+sinx^2))的α次方,x趋0则sinx+sinx^2也趋0。趋0泰勒展开直接用麦克劳林公式套用(1+x)的α次方的麦克劳林公式即1+αx+α(α-1)/2 * x2x为sinx+sinx^2 α为1/2因为分母是sinx平方,所以展开至第三项即可。
根号下函数怎么用泰勒公式
当然可以
f(x)=f(x0)+f'(x0)*(x-x0)+f''(x0)/2*(x-x0)^2+f'''(x0)/6*(x-x0)^3+……
那么f'(x)=1/ 2根号x
f''(x)= -1/4 x^(-3/2)
以此类推得到
fn(x)= (-1)^(n-1)[1*3*5*...*(2n-3)]/2^n *x^(1/2-n)
代入就得到了根号x的泰勒公式展开