函数的焦点是什么

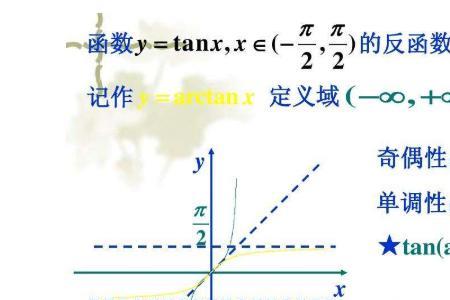
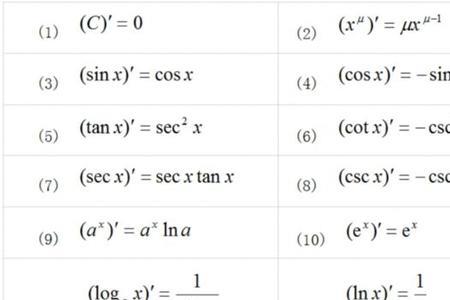几何上圆锥曲线中的抛物线就是二次函数，曲线上的任意一点到一定点的距离等于到一定直线的距离相等，这样的的点的轨迹是抛物线．定点就是焦点，定直线是准线．

有四种形式，建立在直角坐标系中

-------------焦点坐标------准线方程

y^2=2Px，------(P/2，0)-------x=-P/2

y^2=-2Px------(-P/2，0)------x=P/2

x^2=2Py-------(0，P/2)-------y=-P/2

x^2=-2Py------(0，-P/2)------y=P/2

函数的焦点是什么

二次函数也就是抛物线，平面上存在一点和一条直线，二次函数上任一点到这个点和这条直线的距离相等。按圆锥曲线统一定义，这点叫作焦点，这条直线叫准线。

不是所有点到这点距离相等，而是任一点到这点与这条直线距离相等，不同点到这点距离一般是不一样的，比如y=0.25x²，这点就是（0，1），直线是 y=-1。

二次函数表达式为y=ax²+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。如果令y值等于零，则可得一个二次方程。该方程的解称为方程的根或函数的零点。

扩展资料：

二次函数的图像是抛物线，但抛物线不一定是二次函数。开口向上或者向下的抛物线才是二次函数。抛物线是轴对称图形。

对称轴与抛物线唯一的交点为抛物线的顶点P。特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）。

二次项系数a决定抛物线的开口方向和大小。当a>0时，抛物线开口向上当a<0时，抛物线开口向下。|a|越大，则抛物线的开口越小|a|越小，则抛物线的开口越大。

一次项系数b和二次项系数a共同决定对称轴的位置。当a与b同号时（即ab>0），对称轴在y轴左侧当a与b异号时（即ab<0），对称轴在y轴右侧