抛物线的交点公式是什么

抛物线的交点公式是什么：

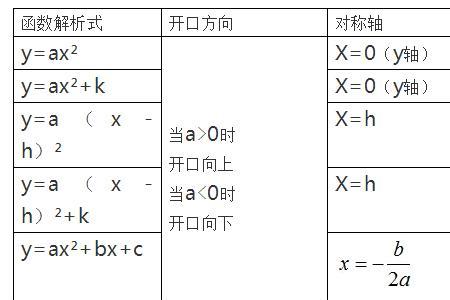
1、一般式:y=aX2+bX+c(a、b、c为常数，a≠0）

顶点式:y=a(X-h）2+k（a、h、k为常数，a≠0）

交点式（两根式）：y=a（x-x1）（x-x2） （a≠0）

其中抛物线y=aX2+bX+c(a、b、c为常数，a≠0）与x轴交点坐标，即方程aX2+bX+c=0的两实数根。

2、抛物线四种方程的异同

共同点：

①原点在抛物线上，离心率e均为1 ②对称轴为坐标轴

③准线与对称轴垂直，垂足与焦点分别对称于原点，它们与原点的距离都等于一次项系数的绝对值的1/4。

不同点：

①对称轴为x轴时，方程右端为±2px，方程的左端为y^2对称轴为y轴时，方程的右端为±2py，方程的左端为x^2

②开口方向与x轴（或y轴）的正半轴相同时，焦点在x轴（y轴）的正半轴上，方程的右端取正号开口方向与x（或y轴）的负半轴相同时，焦点在x轴（或y轴）的负半轴上，方程的右端取负号。

切线方程：

抛物线y2=2px上一点（x0，y0）处的切线方程为： 

抛物线y2=2px上过焦点斜率为k的方程为：y=k（x-p/2）。

抛物线的交点公式是什么

抛物线y=ax²+bx+c 与x轴的交点坐标为（(-b±√Δ)/2a，0） 【Δ为ax²+bx+c=0判别式 Δ=b²-4ac】这之中，实际只是令 y=0 ，求x此时的取值，并视之为横坐标，取纵坐标为0，即得交点坐标