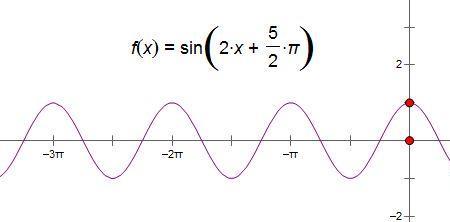
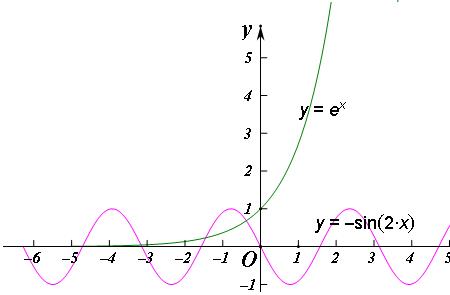
不是
正弦曲线与抛物线是本质上完全不同的两种曲线。有若干种论据可以说明这一点:
(1)正弦曲线是超越曲线,而抛物线是代数曲线。
(2)(反证)假设正弦曲线在区间〔0,pi〕上的部分是一段抛物线,则抛物线的顶点是(pi/2,1),因此这个抛物线的方程是y=A*(x-pi/2)^2+1。把原点的坐标代入,解得A=-4/(pi^2)。但是正弦线上的点(pi/6,1/2)不满足这个抛物线方程,矛盾。
(3)(反证)假设正弦曲线在区间〔0,pi〕上的部分是一段抛物线,这段抛物线的方程是y=A*x^2+B*x+C。则有恒等式
sin(x)-(A*x^2+B*x+C)=0
此式两边各求导数2次,得到
-sin(x)-2*A=0,sin(x)=-2*A
换言之,sin(x)在区间〔0,pi〕上恒等于一个常数,矛盾。