π/2是有理数还是无理数

无理数。

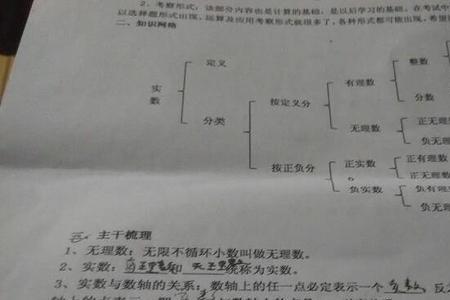
无理数的定义是，无限不循环小数叫无理数。这个定义有两层含义“小数”，“无限不循环”。

假设π/2不是无理数，则他是有理数那么π/2是整数或分数，π/2显然不能被2整除，只能是分数。分数可以化成有限小数或无限循环小数，但π/2既不能化成有限小数，也不能化成无限循环小数。这个矛盾说明假设不成立。所以π/2是无理数。

π/2是有理数还是无理数

无理数，因为π是无限不循环小数，属于无理数。

四种常见的无理数

一是无限不循环小数，例如：0.01001000100001……等

二是根式，例如：√2，√3，（√5-1）/2等

三是函数式，例如：lg2，sin1度等

四是专用符号，如π、e、y。

无理数在位置数字系统中表示（例如，以十进制数字或任何其他自然基础表示）不会终止，也不会重复，即不包含数字的子序列。例如，数字π的十进制表示从3.141592653589793开始，但没有有限数字的数字可以精确地表示π，也不重复。

π/2是有理数还是无理数

π/2当然是无理数！反证法如果π/2是有理数，π/2=p/q（p，q整数，q≠0）π=2p/q=>π是有理数错误所以，π/2是无理数！