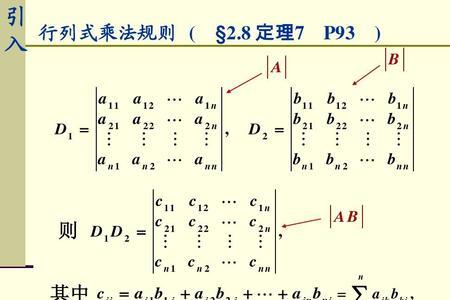
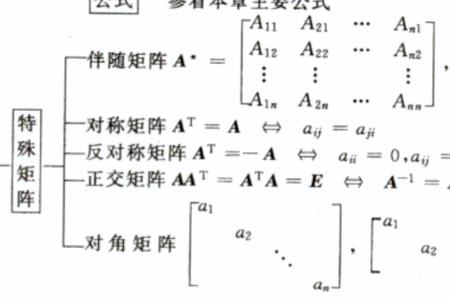
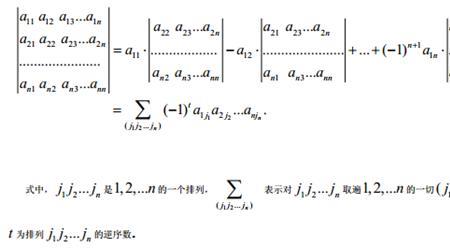
行列式为0的矩阵是不可递的。矩阵可逆的条件是AB=BA=E。矩阵可逆是指一个矩阵拥有对应的递矩阵的情况。在线性代数中,给定一个n阶矩阵A,若存在一个n阶矩阵B使得AB=BA=E,或AB=E,BA=E,其中En阶单位矩阵,只要任意满足一个,则称A是可逆的。
行列式为0的矩阵是可逆矩阵吗
这里是你解错了该矩阵的行列式为 -1,而不是0所以这个矩阵式可逆的记住一点,行列式为0的方阵一定是不可逆的AA^(-1)=E两边取行列式得到|A| |A^(-1)|=1于是|A^(-1)|=1/|A||A|=0时,|A^(-1)|为无穷大,这当然是错的