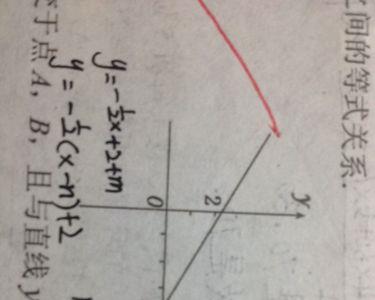函数值恆为1。
其实这个命题没有什么意义。
根据函数的定义,对于自变量X的每一个确定值,依据对应法则,函数y有且只有唯一个值与此对应。因此当自变量×取定一个允许值时,只能在有函数图像上一个相对应点。而一个点要表敍成轴对称形式,那么这个点只在对称轴上。因此这个函数只能是恒等于I的常量函数。
当然函数的图像f(X)可能关于直线X=1对称,其满足的条件是:
对于定义域内任意X值,恒有
f(2—X)=f(X)
恒成立。
事实上,在函数定义域内任取X。,且2—X。也在定义域内,由于
f(2一X。)=f(X。)
则很容易证明两点P(X。,f(X。))和Q(2—X。,f(2—X。))关于直线X=1对称。
由于[X。十(2一X。)]/2
=1,又f(X。)=f(2—X。),所以线段PQ的中点在直线X=1上。又PQ两点纵坐标相,所以PQ⊥直线X=1。
事实上,若函数y=f(X)关于直线X=a对称,则必有f(2a一X)=f(X)
也可以表f敍为
f(a十X)=f(a一X)