第三定义是平面内动点与两定点连接两斜率乘积为常数，（常数为正值b^2/a^2）解设动点p（x，y）定点A（一a，0）B（a，0）则两斜率乘积y^2/（X^2一a^2）=b^2/a^2所以a^2y^2=b^2（X^2一a^2）即X^2/a^2一y^2/b^2=1。注常数是一b^2/a^2曲线是椭圆。
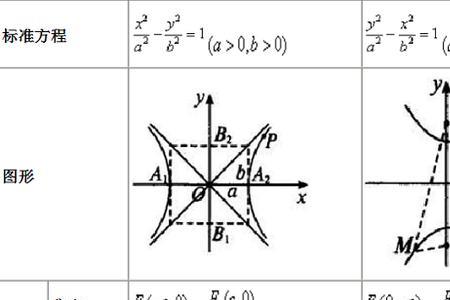
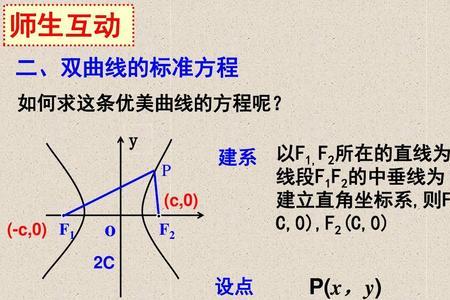
双曲线第三定义推导
原创 | 2023-01-01 13:56:59 |浏览：1.6万
猜你想问
-
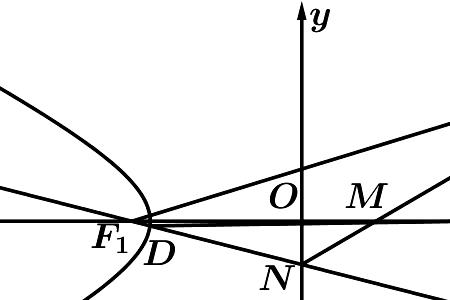双曲线谁最大 双曲线中的a，b，c∈（0，＋∞）。C是最大。因为C＾2＝a＾2十b＾2。c是直角三角形斜边。此关系式来源是在双曲线方程推导过程中把分母c＾2－a＾2用b＾2代替而得关系式。... -
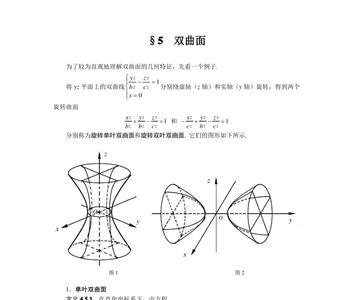双曲线旋转方程 前者叫单叶双曲面，后者叫双叶双曲面。绕某轴旋转，方程中该字母不变，另一字母的平方变成两个字母的平方和。如绕x轴旋转，x^2不变，y^2变成y^2+z^2X=xcosa+ysina，Y=ycosa-x... -
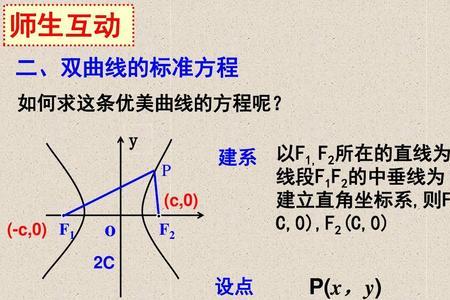求双曲线方程的五种方法 一、直接法由题设所给的动点满足的几何条件列出等式，再把坐标代入并化简，得到所求轨迹方程，这种方法叫做直接法。二、定义法由题设所给的动点满足的几何条件，经过化简... -
双曲线方程成立的条件 先看充分性当“abc＜0”成立时，取a=b=1，c=-1此时曲线ax2+by2=c为x2+y2=-1，不能表示任何曲线∴“abc＜0”不是“曲线ax2+by2=c为双曲线”的充分条件再看必要性当“曲线ax2... -
等轴双曲线的标准方程 X＾2一y＾2＝入（入≠0）当入＞0时焦点在X轴，入＜0时焦点在y轴。等轴双曲线是实轴与虚轴相等双曲线（即a＝b）以y＝±X，离心率e＝√2 等轴双曲线的标准方程 等轴双曲线是实轴和虚轴相等的，即2...
