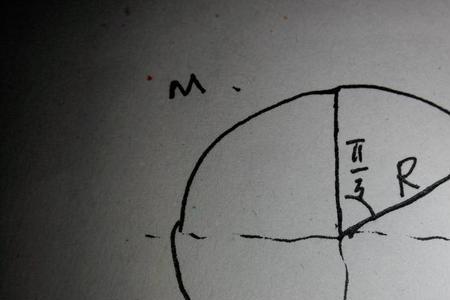
圆周角定理:圆周角等于同弧所对圆心角一半。证明分三类①圆心在边上②圆心在角内部③圆心在角外部。推论一同弧所对圆周角相等。推论二直径所对圆周角为直角。
圆周角定理及推论证明
关注
圆周角定理:一条弧所对圆周角等于它所对圆心角的一半
证明:已知在⊙O中,∠BOC与圆周角∠BAC同对弧BC,求证:∠BOC=2∠BAC。
如图,当圆心O在∠BAC的一边上时,即A、O、B在同一直线上时:OA、OC是半径解:OA=OC∠BAC=∠ACO(等边对等角
1、圆周角
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
2、圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等同圆或等圆中,相等的圆周角所对的弧也相等。
推论2:半圆(或直径)所对的圆周角是直角90°的圆周角所对的弦是直径。
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形