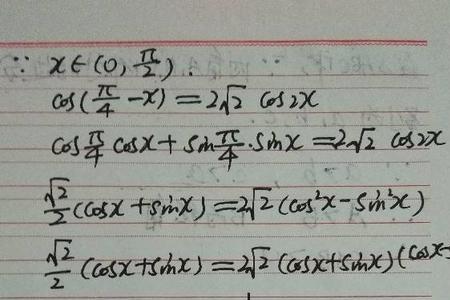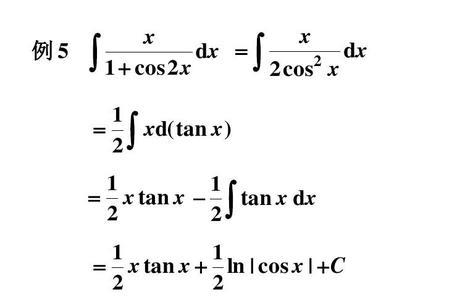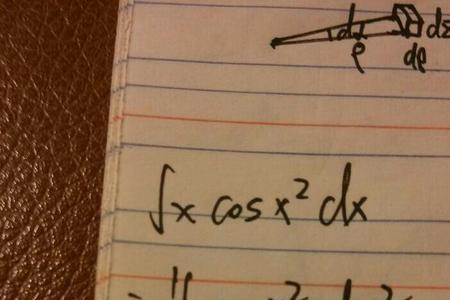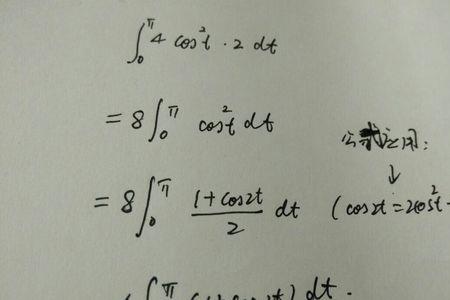cos²x×sin²x=

sin平方x乘以cos平方x等于1。

sinx函数，即正弦函数，三角函数的一种。正弦函数是三角函数的一种。对于任意一个实数x都对应着唯一的角（弧度制中等于这个实数），而这个角又对应着唯一确定的正弦值sinx。

对于任意一个实数x都有唯一确定的值sinx与它对应，按照这个对应法则所建立的函数，表示为y＝sinx，叫做正弦函数。COS即COS函数，全称cosine，适用于求三角形角度等。

Cos函数取某个角并返回直角三角形两边的比值。此比值是直角三角形中该角的邻边长度与斜边长度之比。结果范围在－1到1之间。

cos²x×sin²x=

1

本题是一个直角三小型的恒等式，cos²x+sin²x＝1，是同角三角函数平方关系，是三角恒等式，对任意角x都满足。 的论证就是三个角为角ABC它们所对应的边是abc，cos²A×sin²A=（a/c）^2+（b/c）^2=（a^2+b^2）/c^2，在直角三角形中，三边的关系满足勾股定理，也就是a^2+b^2=c^2，根据等两代换，可以得到cos²x+sin²x=1

cos²x×sin²x=

sin²xcos²x

=1/4×（2sinxcosx）²

=1/4×sin²（2x）

=sin²（2x）/4

积化和差公式：

sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]

cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]

cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]

sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]

和差化积公式：

sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]

sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]

cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]

cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]