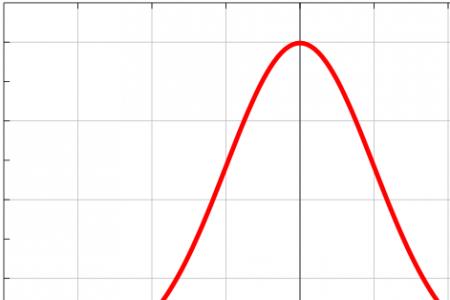
正态分布的拐点就是函数曲线突然方向性变化的点,即二阶导数的零点,有两个拐点,分别在μ±σ处有拐点。
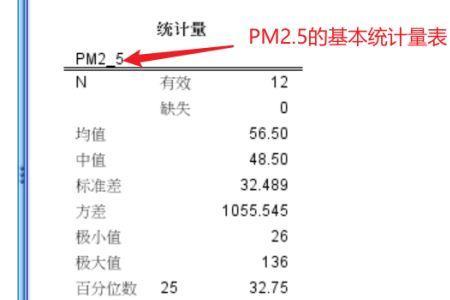
正态分布具有两个参数μ和σ2的连续型随机变量,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ2是此随机变量的方差,所以正态分布记作N(μ,σ2 )。
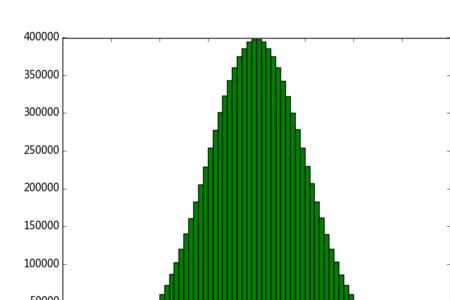
服从正态分布的随机变量的概率规律为取 μ邻近的值的概率大 ,而取离μ越远的值的概率越小σ越小,分布越集中在μ附近,σ越大,分布越分散。
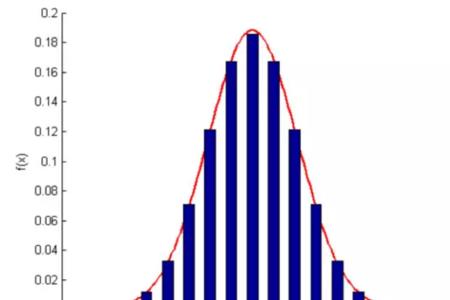
正态分布的密度函数的特点是:关于μ对称,在μ处达到最大值,在正(负)无穷远处取值为0,在μ±σ处有拐点。
它的形状是中间高两边低 ,图像是一条位于x轴上方的钟形曲线。当μ=0,σ2 =1时,称为标准正态分布,记为N(0,1)。