如果不独立,根号下还要加上一个2ρσx*σy。ρ为x,y相关性系数。
因为正态分布知道了EX和DX就可以知道概率密度函数,那么求EX DX就是突破口
设两个变量分别为X,Y,那么E(X+Y)=EX+EYE(X-Y)=EX-EY
D(X+Y)=DX+DYD(X-Y)=DX+DY。
D(X-Y)=D{ X+(-1)* Y } = D(X)+ (-1)^2*D ( Y )=D(X)+ D ( Y )
说明:由于X,Y相互独立,所以交叉项目COV(X,Y)=0
扩展资料:
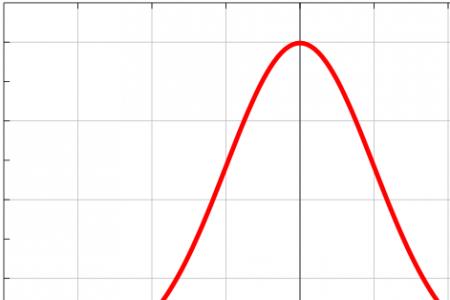
由于一般的正态总体其图像不一定关于y轴对称,对于任一正态总体,其取值小于x的概率。只要会用它求正态总体在某个特定区间的概率即可。
为了便于描述和应用,常将正态变量作数据转换。将一般正态分布转化成标准正态分布。
服从标准正态分布,通过查标准正态分布表就可以直接计算出原正态分布的概率值。故该变换被称为标准化变换。(标准正态分布表:标准正态分布表中列出了标准正态曲线下从-∞到X(当前值)范围内的面积比例。)