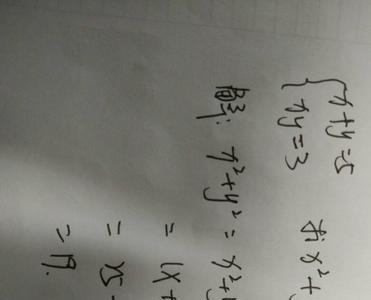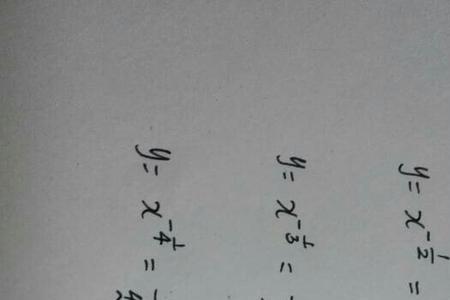答案y=2的x次方减一在实数集上是单调递增的。
说明因为2大于1,这样的指数函数是增函数,他的定义域是全体实数。仅供参考。
y=2的x次方减一的单调性
y=2的x次方减一单调性如下
y=2^1/(x-1),定义域为(-∞,0)∪(0,+∞)
在(-∞,0)和(0,+∞)都是单调递减,而作为指数函数的底2>1,是增函数。
根据复合函数“同增异减”的性质
y=2的x次方减一的单调性
y=|2^x-1|在区间(-无穷,0)上是减函数
在区间(0,+无穷)上是增函数
函数y=2的x次幂-1的绝对值在区间(k-1,k+1)内部单调
所以
(1)k+1<=0 k<=-1
(2) k-1>=0 k>=1
函数y=2的x次幂-1的绝对值在区间(k-1,k+1)内部单调
则k的取值范围是(-无穷,-1]∪[1,+无穷)