矩阵(算子)对应于一个空间中的子空间(平面),取逆和取对偶(转置)变成一个空间上的简单变换。这两个变换是显然可交换的。
对了,矩阵的对偶是转置在复数域上的推广,一个矩阵的对偶是取转置后取复数共轭。一个实矩阵的对偶和转置是一样的。
转置是行变成列列变成行,没有本质的变换
逆矩阵是和这个矩阵相乘以后成为单位矩阵的矩阵
这个是一个本质的变换,逆矩阵除了一些显然的性质以外还有一些很特殊的性质,例如无论左乘还是右乘原矩阵,都是单位矩阵

原创 | 2022-12-07 21:32:37 |浏览:1.6万
矩阵(算子)对应于一个空间中的子空间(平面),取逆和取对偶(转置)变成一个空间上的简单变换。这两个变换是显然可交换的。
对了,矩阵的对偶是转置在复数域上的推广,一个矩阵的对偶是取转置后取复数共轭。一个实矩阵的对偶和转置是一样的。
转置是行变成列列变成行,没有本质的变换
逆矩阵是和这个矩阵相乘以后成为单位矩阵的矩阵
这个是一个本质的变换,逆矩阵除了一些显然的性质以外还有一些很特殊的性质,例如无论左乘还是右乘原矩阵,都是单位矩阵

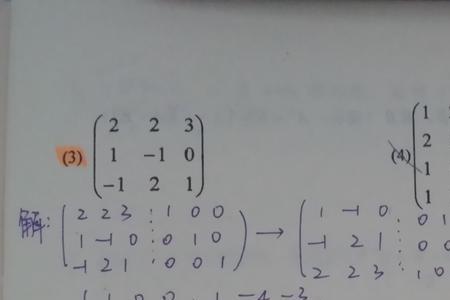


Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com