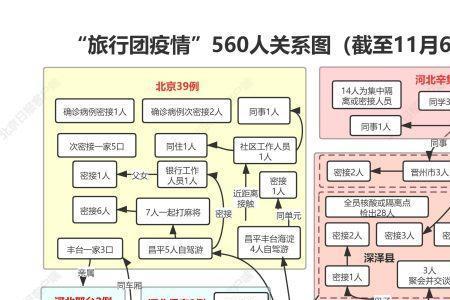
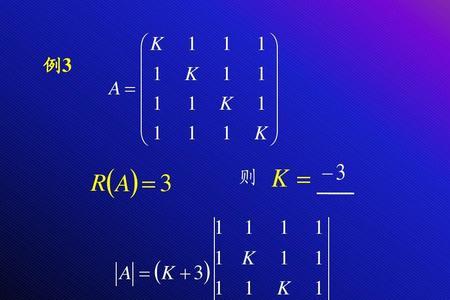R是一个交换环,A是一个以R中元素为系数的n×n的矩阵。A的伴随矩阵可按如下步骤定义:
定义:A关于第i行第j列的余子式(记作Mᵢⱼ)是去掉A的第i行第j列之后得到的(n−1)×(n−1)矩阵的行列式。
定义:A关于第i行第j列的代数余子式是:
Cᵢⱼ=(−1)ⁱ⁺ʲMᵢⱼ。
定义:A的余子矩阵是一个n×n的矩阵C,使得其第i行第j列的元素是A关于第i行第j列的代数余子式。
引入以上的概念后,可以定义:矩阵A的伴随矩阵是A的余子矩阵的转置矩阵:
adj(A)=Cᐪ
也就是说,A的伴随矩阵是一个n×n的矩阵(记作adj(A)),使得其第i行第j列的元素是A关于第j行第i列的代数余子式。简言之,伴随矩阵就是把原来矩阵每一行的代数余子式竖着写:
[adj(A)]ᵢⱼ=Cⱼᵢ。
例子
2x2矩阵
2x2矩阵:
伴随矩阵
它的伴随矩阵:
伴随矩阵