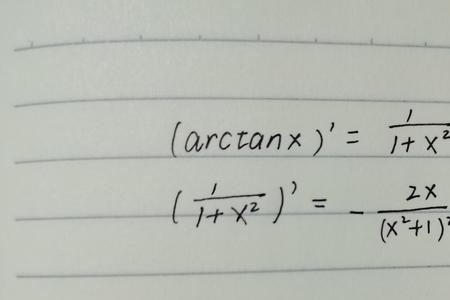arctanx方可以化成什么

因为arctanx等价于x是当x趋近于0的时候arctanx才等价于x

当x趋近于正无穷是arctanx等于π/2

当x趋近于负无穷是arctanx等于-π/2

所以不等价与x(∞)

利用等价无穷小替换求极限时要特别注意趋近过程

扩展资料：

若关系R在集合A中是自反、对称和传递的，则称R为A上的等价关系。所谓关系R 就是笛卡尔积 A×A 中的一个子集。

A中的两个元素x，y有关系R，如果(x，y)∈R。常简记为 xRy。

自反： 任意x属于A，则x与自己具有关系R，即xRx

对称： 任意x，y属于A，如果x与y具有关系R，即xRy，则y与x也具有关系R，即yRx

传递： 任意x，y，z属于A，如果xRy且yRz，则xRz

x，y具有等价关系R，则称x，y R等价，有时亦简称等价

arctanx方可以化成什么

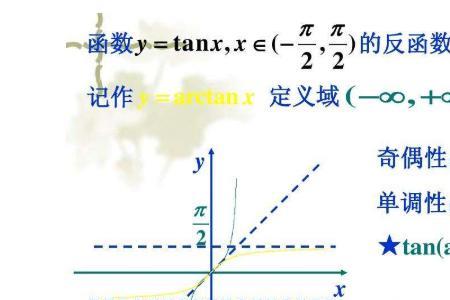
tanx是正切函数，其定义域是{x|x≠(π/2)+kπ，k∈Z}，值域是R。arctanx是反正切函数，其定义域是R，反正切函数的值域为（-π/2，π/2）。两者的转换公式为y=tanxx=arctany。

arctanx和tanx两者的区别：

1、两者的周期性不同

（1）tanx为周期函数，最小正周期为π。

（2）arctanx不是周期函数。

2、两者的单调区间不同

（1）tanx有单调区间(-π/2+kπ，+π/2+kπ)，k为整数，且在该区间为单调增函数。

（2）arctanx为单调增函数，单调区间为（－∞，﹢∞）

arctanx=1/(1+x²)。anx是正切函数，其定义域是{x|x≠(π/2)+kπ，k∈Z}，值域是R。arctanx是反正切函数，其定义域是R，反正切函数的值域为（-π/2，π/2）。

tanx与arctanx的区别

1、两者的定义域不同

（1）tanx的定义域为{x|x≠(π/2)+kπ，其中k为整数}。

（2）arctanx的定义域为R，即全体实数。

2、两者的值域不同

（1）tanx的值域为R，即全体实数。

（2）arctanx的值域为(-π/2，π/2)。