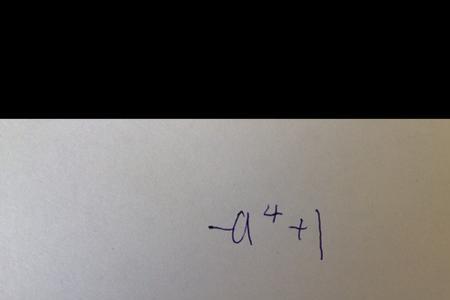1+3+5+n公式怎么来的

1+3+5+7+……+n=（1+n）²/4

计算过程如下：

1=1²

1+3=2²

1+3+5=3²

所以有

1+3+5+7+9+……+n=（1+n）²/4

等差数列：

从第二项起，每一项与它的前一项的差等于同一个常数的一种数列，常用A、P表示。这个常数叫做等差数列的公差，公差常用字母d表示。

例如：1，3，5，7，9……2n-1，项公式为：an=a1+(n-1)*d，首项a1=1，公差d=2。

前n项和公式为：Sn=a1*n+[n*(n-1)*d]/2或Sn=[n*(a1+an)]/2，以上n均属于正整数。

1+3+5+n公式怎么来的

这是一个等差数列。因为等差数列的求和公式是首项加末项乘以项数除以二，因此1+3+5十…十n等于1+n的和乘以n再除以2。