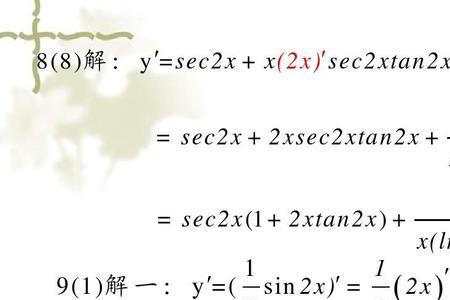tan 2x的倍角公式

tan2x＝sin2x／cos2x，由正弦函数和余弦函数的倍角公式展开得：tan2x＝2sinxcosx／（cos＾2x一sin＾2x），分子分母同时除于cos＾2x得：tan2x＝（2sinx／cosx）／1－（sin＾2x／cos＾2x）＝2tanx／1－tan＾2x。二倍角正切也可以由两角和正切公式导出：tan（A＋B）＝（tanA＋tanB）／（1一tanAtanB），令A＝B＝x得tan2x＝2tanx／（1－tan＾2x）。

tan 2x的倍角公式

   tan2x等于2tanx除以1减去(tanx)的平方

   因为tan2x＝sin2x/cos2x

 这里分子 sin2x＝2sinxcosx

  分母cos2x等于2乘以cosx的平方减去1

   分子、分母都除以(cosx)的平方，得分子是2sinx除以cosx，也就是2tanx。

分母是2减去(cosx)平方分之1，也就是2-(setx)的平方，即

1-（tanx）的平方，因此

tan2x＝2tanx/1-(tanx)的平方