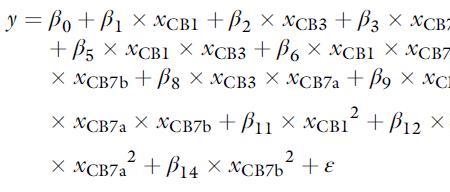这不叫绝对值,叫模,是和向量的大小。
a=(x1,y1) b=(x2,y2)
a+b =(x1+x2,y1+y2)
所以|a+b|=根号[(x1+x2)^2+(y1+y2)^2]
或者
|a+b|^2= (a+b)^2=a^2+2ab+b^2
切记,这里的a和b都是向量。
=|a|^2+2|a||b|cos夹角 +|b|^2
扩展资料
向量的性质
向量的模的运算没有专门的法则,一般都是通过余弦定理计算两个向量的和、差的模。
多个向量的合成用正交分解法,如果要求模一般需要先算出合成后的向量。
模是绝对值在二维和三维空间的推广,可以认为就是向量的长度。推广到高维空间中称为范数。
a加b的绝对值公式
a加b的绝对值等于:
1,a+b≥0时▏a+b▏=a+b,因为正数和零的绝对值是它的本身。
2,a+b<0时▏a+b▏=-(a+b)=⁻a⁻b,因为负数的绝对值是它的相反数。