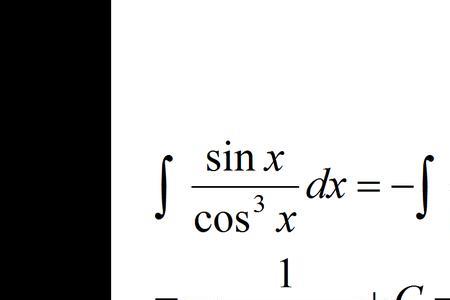解:积分secxdx
=ln/secx+tanx/+C
有好几种方法的:最常用的是∫ secx dx = ln|secx + tanx| + C
第一种最快:
∫ secx dx
= ∫ secx • (secx + tanx)/(secx + tanx) dx
= ∫ (secxtanx + sec²x)/(secx + tanx) dx
= ∫ d(secx + tanx)/(secx + tanx)
= ln|secx + tanx| + C
第二种:
∫ secx dx
= ∫ 1/cosx dx = ∫ cosx/cos²x dx = ∫ dsinx/(1 - sin²x)
= (1/2)∫ [(1 - sinx) + (1 + sinx)]/[(1 - sinx)(1 + sinx)] dsinx
= (1/2)∫ [1/(1 + sinx) + 1/(1 - sinx)] dsinx
= (1/2)[ln|1 + sinx| - ln|1 - sinx|] + C
= (1/2)ln|(1 + sinx)/(1 - sinx)| + C
= ln| √(1 + sinx)/√(1 - sinx) | + C
= ln| [√(1 + sinx)]²/√[(1 - sinx)(1 + sinx)] | + C
= ln| (1 + sinx)/cosx | + C
= ln|secx + tanx| + C
第三种:
∫ secx dx = ∫ 1/cosx dx
= ∫ 1/sin(x + π/2) dx,或者化为1/sin(π/2 - x)
= ∫ 1/[2sin(x/2 + π/4)cos(x/2 + π/4)] dx,分子分母各除以cos²(x/2 + π/4)
= ∫ sec²(x/2 + π/4)/tan(x/2 + π/4) d(x/2)
= ∫ 1/tan(x/2 + π/4) d[tan(x/2 + π/4)]
= ln|tan(x/2 + π/4)| + C
他们的答案形式可以互相转化的