幂函数y=x^a(a∈R),高中只研究a为有理数时的性质与图像。幂函数有两个共同性质:一是函数图像都过(1,1)点二是在(0,+∞)上是单调函数(递增或递减)。a>0时,幂函数y=x^a在(0,+∞)上是单调递增函数a<0时,幂函数y=x^a在(0,+∞)上是单调递减函数。
当a>0时,幂函数的定义域包含数0。
当a<0时,-a>0,此时,y=x^a=1/〈x^(-a)〉,x在分母中,所以,x不可以为0。
原创 | 2022-12-05 13:34:56 |浏览:1.6万
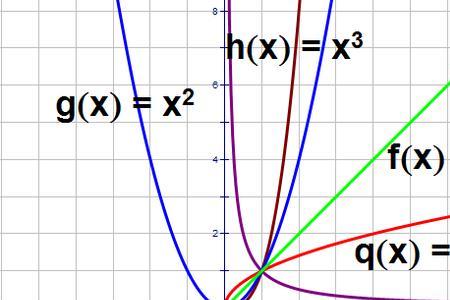
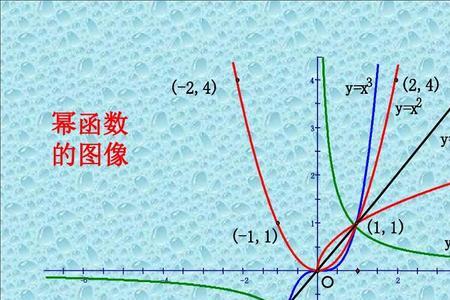
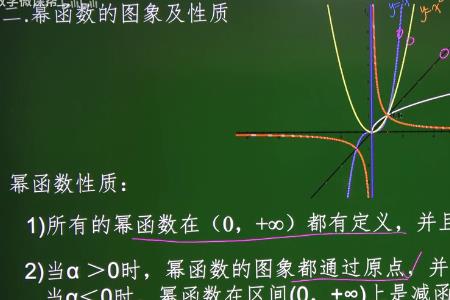
幂函数y=x^a(a∈R),高中只研究a为有理数时的性质与图像。幂函数有两个共同性质:一是函数图像都过(1,1)点二是在(0,+∞)上是单调函数(递增或递减)。a>0时,幂函数y=x^a在(0,+∞)上是单调递增函数a<0时,幂函数y=x^a在(0,+∞)上是单调递减函数。
当a>0时,幂函数的定义域包含数0。
当a<0时,-a>0,此时,y=x^a=1/〈x^(-a)〉,x在分母中,所以,x不可以为0。


Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com