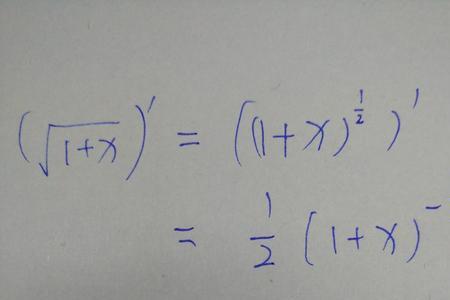根号下cos2x的导数

cos2x的导数：-2sin2x。这是一个复合函数的导数，有两层，外层是cos的导数，内层是2x的导数，所以(cos2x)'=-sin2x*(2x)的导数=-2sin2x。

解：(cos2x)'

=-sin2x*(2x)'

=-2sin2x

导数，也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。

根号下cos2x的导数

所求的导数是：-sin2x／√cos2x。

这是个复合函数求导问题。

第一步：先对cos2x的1／2方求导得：

（1／2）cos2x的（-1/2）次方•cos2x的导数。

第二个步：再对cos2x求导：

（1／2）cos2x的（-1/2）次方•（-sin2x）•（2x）的导数。

第三步：再对2x求导：

（1／2）cos2x的（-1/2）次方•（-sin2x）•2＝-sin2x•cos2x的（-1/2）次方＝-sin2x／√cos2x。

即根号下cos2x的导数＝-sin2x／√cos2x。