没有其它向量极化恒等式口诀,只有以下答案。极化恒等式是联系内积与范数的一个重要的等式,是用范数表示内积的公式。设H是内积空间,‖·‖是由内积(·,·)导出的范数,下列等式常被称为极化恒等式:
当H是实空间时,(x,y)=(1/4)(‖x+y‖2-‖x-y‖2)当H是复空间时,(x,y)=(1/4)(‖x+y‖2-‖x-y‖2+i‖x+iy‖2-i‖x-iy‖2)。
对于实内积空间上的双线性埃尔米特泛函以及复内积空间上的双线性泛函φ(x,y)也分别有类似于上述的恒等式。
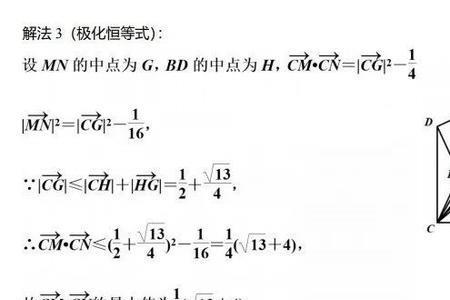
原创 | 2022-12-05 10:29:35 |浏览:1.6万
没有其它向量极化恒等式口诀,只有以下答案。极化恒等式是联系内积与范数的一个重要的等式,是用范数表示内积的公式。设H是内积空间,‖·‖是由内积(·,·)导出的范数,下列等式常被称为极化恒等式:
当H是实空间时,(x,y)=(1/4)(‖x+y‖2-‖x-y‖2)当H是复空间时,(x,y)=(1/4)(‖x+y‖2-‖x-y‖2+i‖x+iy‖2-i‖x-iy‖2)。
对于实内积空间上的双线性埃尔米特泛函以及复内积空间上的双线性泛函φ(x,y)也分别有类似于上述的恒等式。



Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com