提法不妥。应改为椭圆标准方程中横纵坐标取值范围。设椭圆标准方程为X平方比a平方十y平方比b平方=1。由于方程左边是两数平方和（平方是非负数）。所以每个平方都小于等于1。即X平方≤a平方，y平方≤b平方。可得-a≤x≤a，-b≤y≤b。即椭圆处在X=a，X=-a，y=b及y=-b四条直线围成矩形区域内。
椭圆方程的值域
原创 | 2022-12-05 09:17:27 |浏览：1.6万
猜你想问
-
cad椭圆无法分解 原因如下：一、文件本身有错误，使用cad的修复功能修复。二、文件内部存在外部参照、不能立刻分解，内部参照（叫做“块”）都能分解。外部参照只有首先绑定----也就是取消... -
CAD多段线能连接椭圆吗 CAD中直线和多段线是可以互转的。1、电脑打开CAD，画一条连续但不连接的直线。2、画好线之后，输入命令PE，按空格键确定命令。3、确定PE命令后，输入多条命令M，按空格键确... -
cad中圆或椭圆能被分解吗 1、椭圆只是一个图元，无法用分解命令X分解2、如果一定要将其打断的话，建议使用BR打断命令来达到要求（当打断的两个点重合时，既可以将线段分开而不去除线段）。3、分解命... -
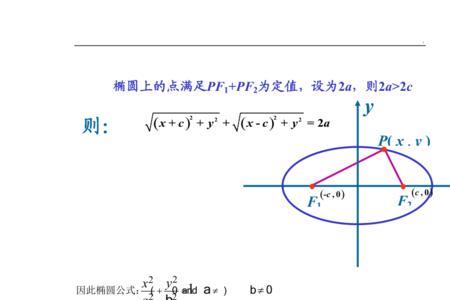椭圆焦半径公式完整推导 椭圆 焦点F1 F2在x轴上的交半径公式的具体推导过程如下：证明：|PF1|²。=(x - c)² + y²。=[a²(x - c)² + a²y²]/a²。=[a²x² - 2a²cx + a²c² + a²y²]/a... -
椭圆焦半径公式cos推导过程 椭圆焦半径公式cos=b2a+ccosθ。cos是余弦，余弦是三角函数的一种。在Rt△ABC（直角三角形）中，∠C=90°，∠A的余弦是它的邻边比三角形的斜边，即cosA=b/c，也可写为cosa=AC/...
