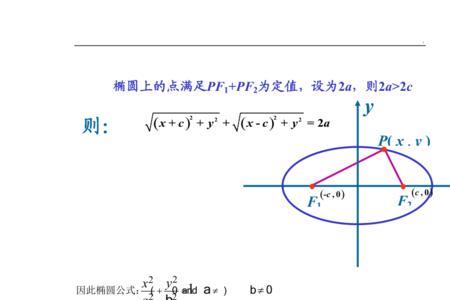
椭圆 焦点F1 F2在x轴上的交半径公式的具体推导过程如下:
证明:
|PF1|²。
=(x - c)² + y²。
=[a²(x - c)² + a²y²]/a²。
=[a²x² - 2a²cx + a²c² + a²y²]/a² /***--根据b²x² + a²y² = a²b² /。
=[a²x² - 2a²cx + a²c² + a²b² - b²x²]/a²。
=[(a²-b²)x² = 2a²cx + a²(b² + c²)]/a²。
=[c²x² -2a²cx + a^4]/a²。
=(a² - cx)²/a²。
∴PF1 = (a² - cx)/a = a - (c/a)x = a - ex。
同理可证:PF2 = a + ex。
椭圆焦半径公式完整推导
点P(x,y)在椭圆上。PF2为焦半径,右边准线为x=a^2/c,由椭圆第二定义, e=PF2/(a^2/c-x),所以PF2=e(a^2/c-x)=a-ex 另一半同理可证。