一个正合数n,对于所有跟n互质的整数b,b^n-b都是n的倍数,那么n就是一个卡迈克尔数。根据费马小定理,所有质数都具备这种特质,因此卡迈克尔数又被称为“伪质数”。
卡迈克尔数是数学界什么难题
卡迈克尔数是数学界难题
"卡迈尔克数"又称"绝对伪素数",这是一道是困扰数学界上百年的重大难题。在数学界算法准确率也不高,对于很多的数学爱好者它都是一个棘手的难题。
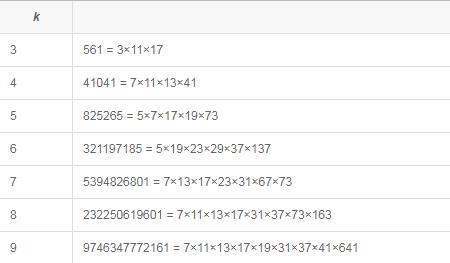
绝对假素数(absolute improper prime number)亦称绝对伪素数,是一类特殊的合数,指对一切整数a,满足n|(an-a)的合数n,由定义知合数n应能整除2n-2,3n-3,4n-4,…,即使a为负整数,n|(an-a)也能成立。从费马定理可以证明561能整除a561-a,又因561=3·11·17,所以561是绝对假素数。已知的绝对假素数还有:2 821,10 585,15 841,至今还不知道是否存在无穷多的绝对假素数。