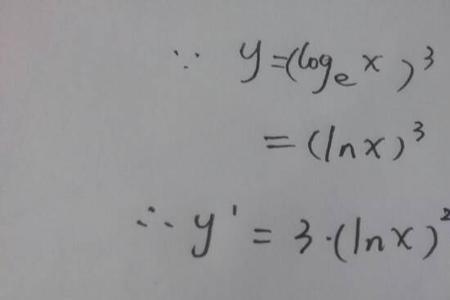e的kx次方求导过程

e的kx次方的导数等于ke^(kx)。设f(x)=e^(kx)，这是一个由一次函数和指数函数一起合成的复合函数，要求它的导数就必须应用复合函数求导数的方法，先把两重函数关系分别求导，再把它们乘在一起便得到原来函数的导数。故y的导数等于e^(kx)✘k=ke^(kx)。

e的kx次方求导过程

对e的负x次幂求导，为什么是负

-e^（-x）。由复合函数求导法则可以简单推得。

e^（-x）可以看成u=-x，y=e^u，对e^（-x）求导的结果就是e^（-x）（-x）'=-e^（-x）。

链式法则：

若h(a)=f[g(x)]则h'(a)=f’[g(x)]g’(x)

链式法则用文字描述，就是“由两个函数凑起来的复合函数，其导数等于里函数代入外函数的值之导数，乘以里边函数的导数。”

扩展资料：

商的导数公式：

(u/v)'=[u*v^(-1)]'

=u' * [v^(-1)] +[v^(-1)]' * u

= u' * [v^(-1)] + (-1)v^(-2)*v' * u

=u'/v - u*v'/(v^2)

通分，易得

(u/v)=(u'v-uv')/v²

常用导数公式：

1、y=c(c为常数) y'=0

2、y=x^n y'=nx^(n-1)

3、y=a^x y'=a^xlna，y=e^x y'=e^x

4、y=logax y'=logae/x，y=lnx y'=1/x

5、y=sinx y'=cosx

6、y=cosx y'=-sinx

7、y=tanx y'=1/cos^2x

8、y=cotx y'=-1/sin^2x以上只提供参考