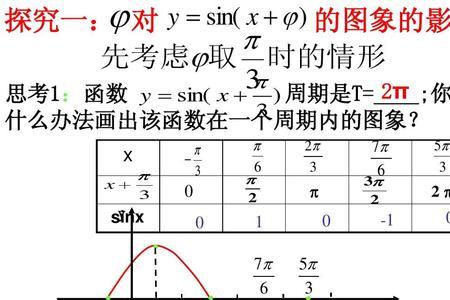
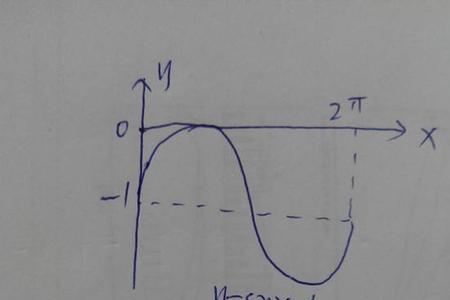
确定正弦型函数中的φ公式:f(x)=Asin(ωx+φ)。正弦型函数是实践中广泛应用的一类重要函数,指函数y=Asin(ωx+φ)(其中A,ω,φ均为常数,且A>0,ω>0)。这里A称为振幅,ω称为圆频率或角频率,φ称为初相位或初相角,正弦型函数y=Asin(ωx+φ)是周期函数,其周期为2π/ω。
函数(function)的定义通常分为传统定义和近代定义,函数的两个定义本质是相同的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合、映射的观点出发。
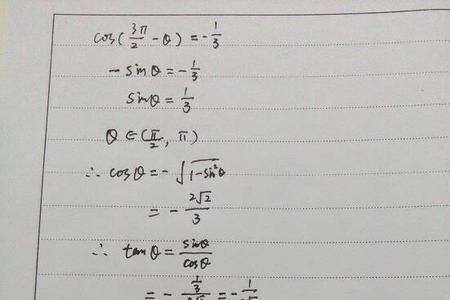
原创 | 2022-12-04 14:19:58 |浏览:1.6万
确定正弦型函数中的φ公式:f(x)=Asin(ωx+φ)。正弦型函数是实践中广泛应用的一类重要函数,指函数y=Asin(ωx+φ)(其中A,ω,φ均为常数,且A>0,ω>0)。这里A称为振幅,ω称为圆频率或角频率,φ称为初相位或初相角,正弦型函数y=Asin(ωx+φ)是周期函数,其周期为2π/ω。
函数(function)的定义通常分为传统定义和近代定义,函数的两个定义本质是相同的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合、映射的观点出发。



Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com