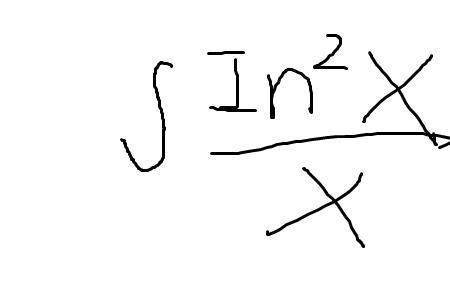lnx的平方的原函数
∫(lnx)^2dx
令u=lnx,则x=e^u dx=e^udu
∫(lnx)^2dx
=∫u^2 e^udu,再用分部积分法
=u^2e^u-∫2ue^udu
=u^2e^u-2[ue^u-∫e^udu]
=u^2e^u-2[ue^u-e^u]+C
=(u^2-2u+2)e^u+C
=[(lnx)^2-2lnx+2)]x+C
扩展资料:
已知函数f(x)是一个定义在某区间的函数,如果存在可导函数F(x),使得在该区间内的任一点都有dF(x)=f(x)dx,则在该区间内就称函数F(x)为函数f(x)的原函数。
已知作直线运动的物体在任一时刻t的速度为v=v(t),要求它的运动规律 ,就是求v=v(t)的原函数。原函数的存在问题是微积分学的基本理论问题,当f(x)为连续函数时,其原函数一定存在