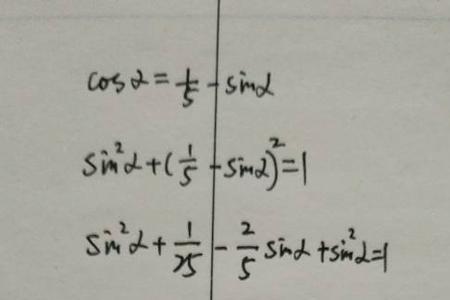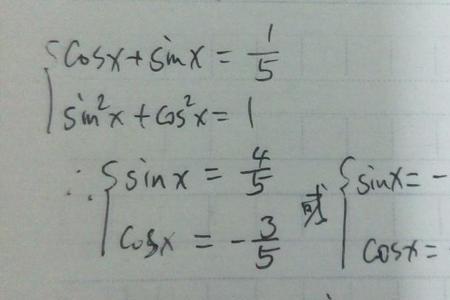cosa的平方加sina的平方

答:(cosA)^2+(sinA)^2=1。(注:通常用大写字母A，B，C表示三角形的三个内角，它们与所对的边同名，即用小写的a，b，c表示，下同)。

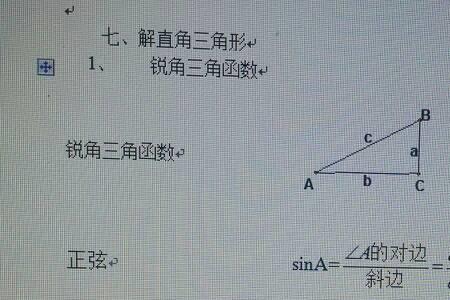
证明:设直角三角形ABC的直角为角C，斜边为c。由锐角三角函数的定义有

sinA=a/c，cosA=b/c，所以

(sinA)^2+(cosA)^2

=(a/c)^2+(b/c)^2

=(a^2+b^2)/c^2。

根据勾股定理，得

a^2+b^2=c^2

∴(sinA)^2+(cosA)^2

=c^2/c^2=1。

这个结结就是同角正，余弦的平方关系。它的应用比较广泛。

例如，已知sinA=3/5，求tanA的值。(角A为锐角)

分析:根据三角函数的商数关系，有

tanA=sinA/cosA。由上述已证明的结论，只要求出cosA即可，因角A为锐角，所以cosA>0。

∴cosA=✔[1-(sinA)^2]

=✔[1-(3/5)^2]

=4/5。

∴tanA=sinA/cosA

=(3/5)÷(4/5)

=3/4。

cosa的平方加sina的平方

①cosA=临边/斜边，sinA=对边/斜边

cosA²+sinA²=（临边²+对边²）/斜边²

②因为 临边²+对边²=斜边²，则为：斜边²/斜边²=1

③可见，该公式与角度大小无关。所以当角度为A/2结果为1

(cosx)^2 + (sinx)^2 =1 x=A (cosA)^2 + (sinA)^2 =1 x=A/2 (cos(A/2))^2 + (sin(A/2))^2 =1

有公式cosa平方+sina平方=1

cos A+sin A = 2^(1/2)*sin(A + 45°) 取值范围为[-2^(1/2)，2^(1/2)]

上面 ^ 符号表示幂，* 表示乘，/ 表示除，2^(1/2) 就表示 “根号 2 ”.