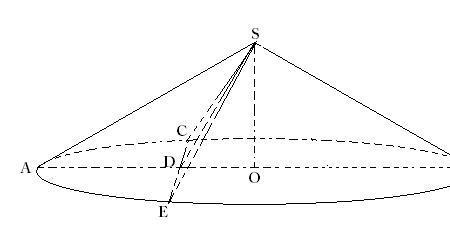
1)圆锥的底面半径为R,内接圆柱的底面半径为3/4R,取轴截面观察,根据三角形相似,可以得出内接圆柱与圆锥的高的比值为1:4,已知圆锥的髙为3R,那么内接圆柱的高为3/4R。根据圆柱体表面积公式可求得:S=2*pi*(3/4R)*(3/4R)pi*2*(3/4R)*(3/4R)=(9/4)R^2(2)解:设内接圆柱底面半径为r,高为h。
则:h/3R=(R-r)/Rh=3(R-r)内接圆柱全面积S=2S1S2=2×r^×π2π×r×h=2π×[r^3rR-3r^]=2π(-2r^3Rr)Smax=2π×[-2×(9/16)×R^(9/4)R^]=2π×[(9/8)R^]=9πR^/4此时:r=3R/4。