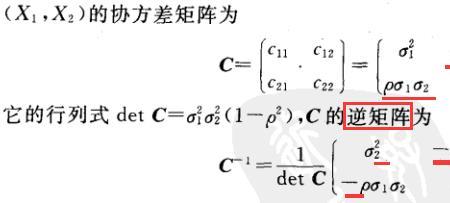
无论矩阵还是向量都没有“方差”的说法,方差是统计学中说随机样本的,如果你向量/矩阵作为随机样本出现,他们的概念则是一致的D(X)= E(X^2)-(E(X))^2,其中E表示求平均值,^2表示求平方,这对于所有样本类型计算都是一样的随机向量对应随机变量方差的数字特征应是协方差阵:D(X)=E{[X-E(X)][X-E(X)]'}其中E(X)为向量均值等于向量每个分量的均值,X-E(X)就是分量减去各自分量的均值,[X-E(X)]'表示转置即行向量。
对角线上元素对应的是每个分量的方差,如果各个分量独立的话,D(X)是对角阵。你说的向量的方差应就是它。
向量方差是什么意思
多元随机变量的问题, 矩阵里面的元素全部是随机变量! 行向量 列向量也一样!
向量的方差,就是指协方差矩阵 !可以参考多元统计分析