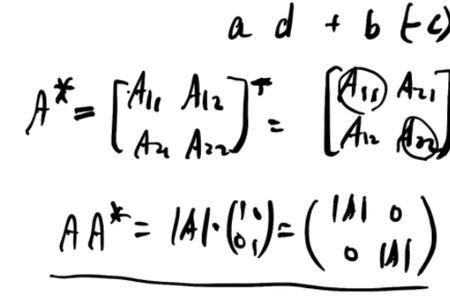设λ是A的特征值,α是A的属于特征值λ的特征向量。
则Aα=λα。
等式两边左乘A*,得
A*Aα=λA*α。
由于A*A=|A|E所以
|A|α=λA*α。
当A可逆时,λ不等于0。
此时有A*α=(|A|/λ)α
所以|A|/λ是A*的特征值。
扩展资料:
求矩阵的全部特征值和特征向量的方法如下:
第一步:计算的特征多项式
第二步:求出特征方程的全部根,即为的全部特征值
第三步:对于的每一个特征值,求出齐次线性方程组:一个基础解系,则的属于特征值的全部特征向量(其中是不全为零的任意实数)。
若是的属于的特征向量,则也是对应于的特征向量,因而特征向量不能由特征值惟一确定。反之,不同特征值对应的特征向量不会相等,亦即一个特征向量只能属于一个特征值。
伴随矩阵特征值的推导
伴随矩阵公式:AA*=|A|E。在线性代数中,一个方形矩阵的伴随矩阵是一个类似于逆矩阵的概念。如果二维矩阵可逆,那么它的逆矩阵和它的伴随矩阵之间只差一个系数,对多维矩阵也存在这个规律。