切线的证明方法和技巧

1、已知条件中直线与圆若有公共点，且存在连接公共点的半径，可直接根据“经过直径的一端，并且垂直于这条直径的直线是圆的切线”来证明。口诀是“见半径，证垂直”。

2、条件中若给出了直线和圆的公共点，但没有给出过这个点的半径，则连结公共点和圆心，然后根据“经过半径的外端且垂直于这条半径的直线是圆的切线”这个定理来证明，口诀是“连半径，证垂直”。

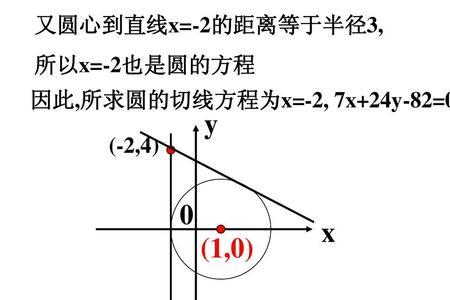
3、已知条件若没有给出了直线和圆的公共点，则过圆心向这条直线引垂线，然后根据“到圆心的距离等于半径的直线是圆的切线”这个定理来证明，口诀是“作垂直，证半径”。

切线的证明方法和技巧

方法一，经过切点垂直于切线的直线必过圆心，切线性质。

方法二，经过圆心垂直于切线的直线必过切点，切线性质。

方法三，切线和圆只有一个公共点，切线性质

方法四，切线和圆心的距离等于圆的半径，切线性质。

方法五，切线垂直于经过切点的半径，切线性质

方法总结

:1.经过切点垂直于切线的直线必过圆心，切线性质.

2、经过圆心垂直于切线的直线必过切点，切线性质。

3、切线和圆只有一个公共点，切线性质.

4、切线和圆心的距离等于圆的半径，切线性质。5.

切线垂直于经过切点的半径，切线性质。