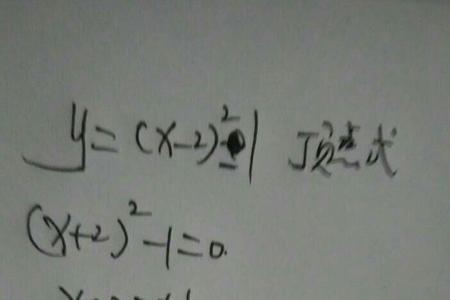是在问二次函数化成顶点式吗
如y=a x²+b x+c
先把a提出来得y=a[x²+b/a x]+c
然后转化成y=a[x+b/2a]²-b²/4a+c
比如y=4x²+6x+8
得y=4[x²+3/2x]+8
得y=4[x+3/4]²-9/4+8
得y=4[x+3/4]²+23/4 顶点为[ -3/4,23/4顶点式:y=a(x-h)²+k, 抛物线的顶点P(h,k)
化为顶点式是:y=a(x+b/2a)²+(4ac-b²)/4a
配方过程如下:y=ax²+bx+c=a(x²+bx/a)+c=a(x²+bx/a+b²/4a²-b²/4a²)+c=a(x+b/2a)²-b²/4a+c=a(x+b/2a)²+(4ac-b²)/4a
扩展资料:
一次项系数b和二次项系数a共同决定对称轴的位置。
当a>0,与b同号时(即ab>0),对称轴在y轴左 因为对称轴在左边则对称轴小于0,也就是- b/2a<0,所以 b/2a要大于0,所以a、b要同号
当a>0,与b异号时(即ab<0),对称轴在y轴右。因为对称轴在右边则对称轴要大于0,也就是- b/2a>0, 所以b/2a要小于0,所以a、b要异号
可简单记忆为左同右异,即当对称轴在y轴左时,a与b同号(即a>0,b>0或a<0,b<0)当对称轴在y轴右时,a与b异号(即a0或a>0,b<0)(ab<0)