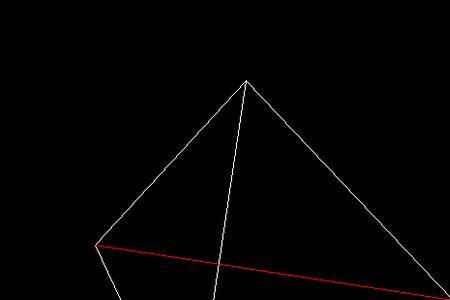
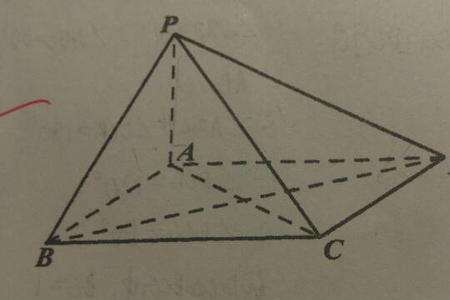
设正四面体P-ABC,底面ABC的高为PO,各棱长为a
∵PA=PB=PC
∴OA=OB=OC,(斜线相等,则其射影也相等)
∴O是正△抄ABC的外心,(重心)
延长OA与BC相交于D
则AD=√3a/2
根据三角形重心的性质
AO=2AD/3=√3a/3
∵△PAO是RT△
∴根据勾股定理
PO^2=PA^2-AO^2
∴PO=√(a^2-a^2/3)= √6a/3
∴正四面体的高为√6a/3.
正四面体的高怎么求
求正四面体的高,要先确定高线在正四面体中的位置。
任选它的一个侧面为底面,由于正四面体是由四个正三角形围成的几何体,那么高线和底面的交点是底面三角形的中心,也是底面正三角形的重心,内心,外心和垂心。这样根据勾股定理就能求出高线。
已知正四面体的棱长为a,那么它底面外接圆半径r就是√3a/3,侧棱、高线h和底面外接圆半径构成一个直角三角形,那么
h²=a²-r²
h=√6a/3。