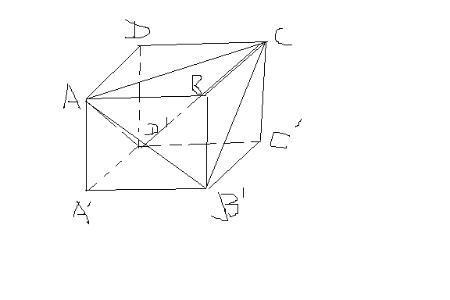
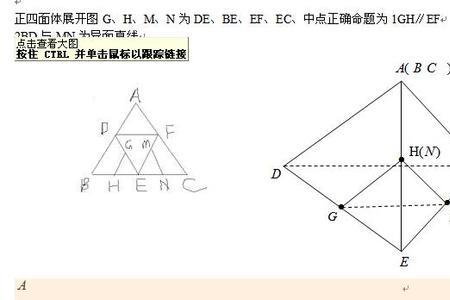
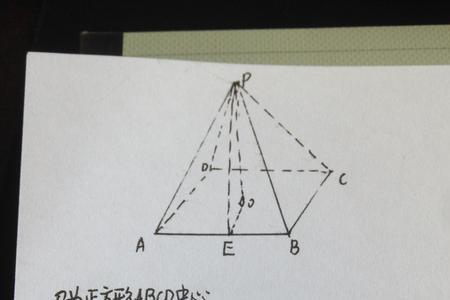
把正四面体ABCD分解成四个小三棱锥。我们知道,平面外一点向平面内三点连线段,则这四点就可以作为三棱柱的四个顶点。首先注意到正四面体有四个全等的三角形:△ABC、△BCD、△CDA、△BDA。在正四面体内任选一点O,连接OA、OB、OC、OD,则O-ABC、O-BCD、O-CDA、O-BDA就是四面体ABCD分解的四个小三棱锥。当O点为正四面体的中心时,则四个小三棱锥是形状一样的正三棱锥。
另外,也可以选择正四面体一个顶点作为小三棱锥的顶点,经过这一点三次截正四面体,截时只要保证底面是三角形就可以。