arcx定义域

arctanx的值

arctanx的值域是：(-π/2，π/2)

正切函数y=tanx在开区间（x∈(-π/2，π/2)）的反函数，记作y=arctanx 或 y=tan-1x，叫做反正切函数。它表示(-π/2，π/2)上正切值等于 x 的那个唯一确定的角，即tan(arctan x)=x，反正切函数的定义域为R即(-∞，+∞)。正切函数是反三角函数的一种。

由于正切函数y=tanx在定义域R上不具有一一对应的关系，所以不存在反函数。注意这里选取是正切函数的一个单调区间。而由于正切函数在开区间(-π/2，π/2)中是单调连续的，因此，反正切函数是存在且唯一确定的。

引进多值函数概念后，就可以在正切函数的整个定义域(x∈R，且x≠kπ+π/2，k∈Z)上来考虑它的反函数，这时的反正切函数是多值的，记为 y=Arctan x，定义域是(-∞，+∞)，值域是 y∈R，y≠kπ+π/2，k∈Z。

(-π/2，π/2)。arctanx是反正切函数，其定义域是R，反正切函数的值域为（-π/2，π/2）。anx是正切函数，其定义域是{x|x≠(π/2)+kπ，k∈Z}，值域是R

arcx定义域

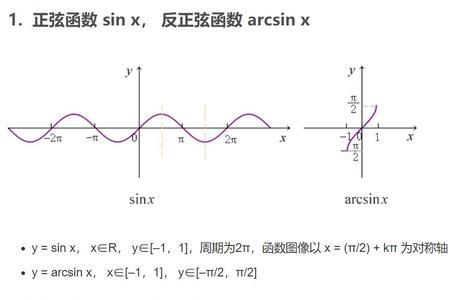
反正弦函数y=arcsinx

表示一个正弦值为x的角，该角的范围在[-π/2，π/2]区间内。

定义域[-1，1] ，值域[-π/2，π/2]。

反余弦函数y=arccosx

表示一个余弦值为x的角，该角的范围在[0，π]区间内。

定义域[-1，1] ， 值域[0，π]。

反正切函数y=arctanx

表示一个正切值为x的角，该角的范围在（-π/2，π/2）区间内。

定义域R，值域（-π/2，π/2）。

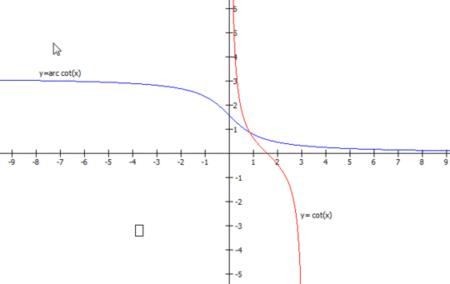
反余切函数y=arccotx

表示一个余切值为x的角，该角的范围在（0，π）区间内。

定义域R，值域（0，π）。

反正割函数y=arcsecx

表示一个正割值为x的角，该角的范围在[0，π/2)U(π/2，π]区间内。

定义域（-∞，-1]U[1，+∞)，值域[0，π/2)U(π/2，π]。

反余割函数y=arccscx

表示一个余割值为x的角，该角的范围在[-π/2，0)U(0，π/2]区间内。

定义域（-∞，-1]U[1，+∞)，值域[-π/2，0)U(0，π/2]。