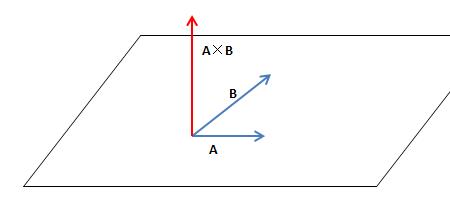
因为平面过直线,则平面的法向量一定垂直于平面内直线的切向量。一个平面垂直于另一个平面,则两个平面的法向量一定垂直。那么,所求平面的法向量既要垂直已知直线的切向量,又要垂直已知平面的法向量,我们知道,只要这两个已知向量不是平行向量或者在同一直线上,这两个已知向量的就可以组成一个平面(向量可以自由平移的特点所决定,等同于把两个异面直线平移到相交直线)那么,垂直这一平面的向量,由这两个已知向量的叉积所决定。因此,取两者的叉积。
因为叉乘的结果是和两个向量都垂直的,恰好是法向量的特征。
原创 | 2022-11-15 15:50:46 |浏览:1.6万
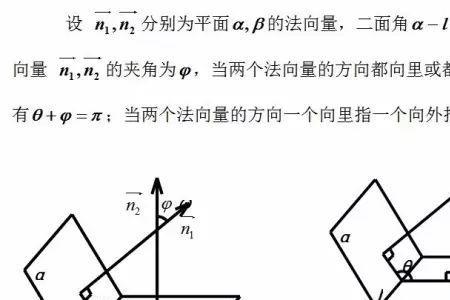
因为平面过直线,则平面的法向量一定垂直于平面内直线的切向量。一个平面垂直于另一个平面,则两个平面的法向量一定垂直。那么,所求平面的法向量既要垂直已知直线的切向量,又要垂直已知平面的法向量,我们知道,只要这两个已知向量不是平行向量或者在同一直线上,这两个已知向量的就可以组成一个平面(向量可以自由平移的特点所决定,等同于把两个异面直线平移到相交直线)那么,垂直这一平面的向量,由这两个已知向量的叉积所决定。因此,取两者的叉积。
因为叉乘的结果是和两个向量都垂直的,恰好是法向量的特征。




Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com