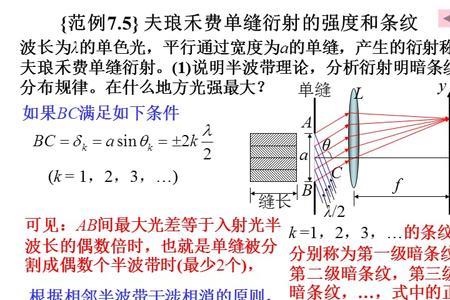
求空间向量的法向量的时候如果法向量的一个坐标没有出来不是可以随便赋值。
求空间向量的法向量的时候如果法向量的一个坐标没有出来,在赋值的时候要保证法向量是非零向量。因为零向量的方向是无法确定的。但我们规定:零向量的方向与任一向量 平行,与任意向量共线,与任意向量垂直。零向量的方向不确定,但模的大小确定。
空间向量
向量规定:向量的大小叫作向量的长度或模。长度为0的向量叫作零向量,记为0。模为1的向量称为单位向量。与向量a长度相等而方向相反的向量,称为a的相反向量。记为-a。方向相等且模相等的向量称为相等向量。
共线向量定理:两个空间向量a,b向量(b向量不等于0),a//b的充要条件是存在唯一的实数λ,使a=λb。共面向量定理。如果两个向量a,b不共线,则向量c与向量a,b共面的充要条件是:存在唯一的一对实数x,y,使c=ax+by。