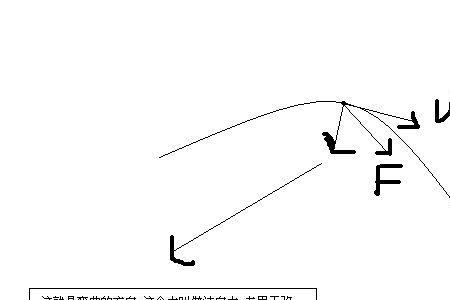
切向量|A|=√a^2+b^2+c^2,曲线在一点处的切向量可以理解为沿曲线该点处切线方向的向量。
切向量是与曲线相切的向量,给定曲线C上一点P,Q是C上与P的邻近一点,当Q点沿曲线趋近于P时,割线PQ的极限位置称为曲线C在P点的切线。
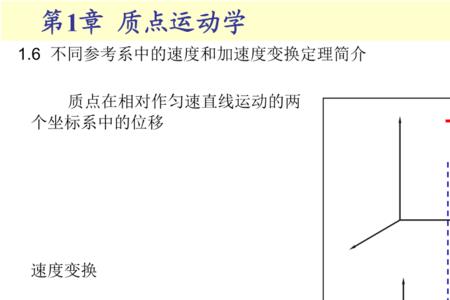
流形的一个特征是它的一个局域可以与一个n维欧氏空间之间建立起点与点间的一对一映射关系,它的每个局域可以分别与各自的一个n维欧氏空间之间建立起点与点间的一对一映射关系,并可在此基础上建立起通用于各局域的流形局部坐标系,从而变成可度量的。

原创 | 2022-11-15 15:50:14 |浏览:1.6万
切向量|A|=√a^2+b^2+c^2,曲线在一点处的切向量可以理解为沿曲线该点处切线方向的向量。
切向量是与曲线相切的向量,给定曲线C上一点P,Q是C上与P的邻近一点,当Q点沿曲线趋近于P时,割线PQ的极限位置称为曲线C在P点的切线。
流形的一个特征是它的一个局域可以与一个n维欧氏空间之间建立起点与点间的一对一映射关系,它的每个局域可以分别与各自的一个n维欧氏空间之间建立起点与点间的一对一映射关系,并可在此基础上建立起通用于各局域的流形局部坐标系,从而变成可度量的。



Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com