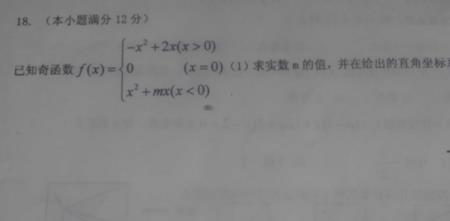奇函数的定义域为R,那么此奇函数一定经过原点(0,0)
对于某些奇函数而言,它在x=0处导数为0
比如f(x)=x^3,因为f'(x)=3x^2,将x=0代入,得f'(x)=0
对于某些奇函数而言,它在x=0处导数不为0
比如f(x)=kx,因为f'(x)=k,在x属于R时,f'(x)恒不为0
对于一个定义域为R的奇函数而言,如果它存在一次项,那么它在x=0处的导数一定不为0
奇函数的导数推导过程
这是定理:奇函数的导数是偶函数,偶函数的导数是奇函数.
证明:设f(x)是奇函数,导数为f'(x).因为f(-x)=-f(x),两边对x求导,有
-f'(-x)=-f'(x),所以f'(-x)=f'(x),所以f'(x)是偶函数.
类似可证偶函数的导数是偶函数.
完毕!