在古代圆柱体积公式并不完全是通过“割补法”获得的。而是一种纯数学的推理,他们把圆柱定义为“圆的均匀分布”,圆柱是由无限个圆组成,但无限个圆又堆积出有限的高度,这种无限中的有限,就渗透着极限与不可分量。
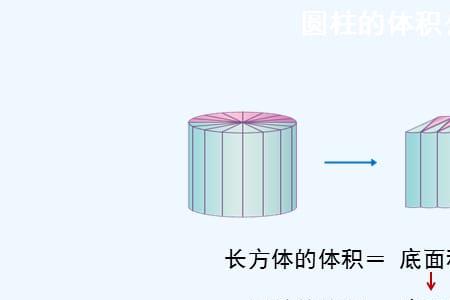
这样看来,圆柱体积就是变成了求圆形面积的数量,而这种求体积的思想又拓展到所有直柱体,以至于所有直柱体的体积都可用“底面积×高”来计算。
原创 | 2022-11-13 16:31:13 |浏览:1.6万
在古代圆柱体积公式并不完全是通过“割补法”获得的。而是一种纯数学的推理,他们把圆柱定义为“圆的均匀分布”,圆柱是由无限个圆组成,但无限个圆又堆积出有限的高度,这种无限中的有限,就渗透着极限与不可分量。
这样看来,圆柱体积就是变成了求圆形面积的数量,而这种求体积的思想又拓展到所有直柱体,以至于所有直柱体的体积都可用“底面积×高”来计算。




Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com