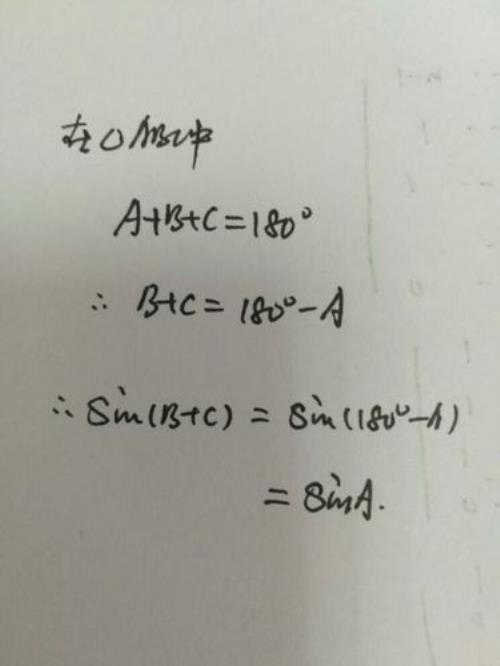c方等于什么公式

在小学数学里表示圆的周长，还有高中数学中的C是复数集、常数。C然后上标一个数下标一个数是组合数，CuA 是全集U中的子集A的补集。这里的希腊字母π，和通常一样代表圆周长和直径的比值，即为圆周率。 现代数学家可以用微积分或更高深的后继理论实分析得到这个面积。

但是在古希腊伟大的数学家阿基米德在《圆的测量》中使用欧几里得几何证明了一个圆周内部的面积等于一个以其圆周长及半径作为两个直角边的直角三角形面积。

c方等于什么公式

若x1，x2，x3......xn的平均数为m则方差

例1 两人的5次测验成绩如下：

X： 50，100，100，60，50 E(X )=72

Y： 73， 70， 75，72，70 E(Y )=72。

平均成绩相同，但X 不稳定，对平均值的偏离大。方差描述随机变量对于数学期望的偏离程度。

单个偏离是消除符号影响方差即偏离平方的均值，记为D(X )：

直接计算公式分离散型和连续型，具体为：这里 是一个数。推导另一种计算公式

得到：“方差等于平方的均值减去均值的平方”。

其中，分别为离散型和连续型的计算公式。 称为标准差或均方差，方差描述波动

性质

1．设C为常数，则D(C) = 0（常数无波动）

2． D(CX )=$C^2$ D(X ) （常数平方提取，C为常数，X为随机变量）

证：特别地 D(-X ) = D(X )， D(-2X ) = 4D(X )（方差无负值）

3．若X 、Y 相互独立，则，证：记

前面两项恰为 D(X )和D(Y )，第三项展开后为

当X、Y 相互独立时，故第三项为零。特别地独立前提的逐项求和，可推广到有限项。