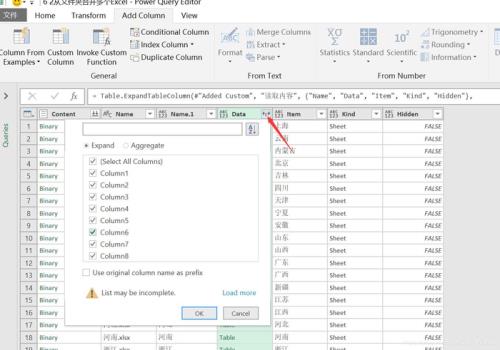
已知OA是面α的一条斜线,OB⊥α。在α内过B作BC⊥AC,垂足为C,连接OC。OA和α所成角∠OAB=θ1,AC和AB所成角∠BAC=θ2,OA和AC所成角∠OAC=θ。求证cosθ=cosθ1*cosθ2
证明:
∵OB⊥α
∴BC是OC在α上的射影
∵BC⊥AC
∴OC⊥AC(三垂线定理)
由三角函数的定义可知
cosθ1=AB/OA,cosθ2=AC/AB,cosθ=AC/OA
∴cosθ1*cosθ2=AB/OA*AC/AB=AC/OA=cosθ
或利用三面角余弦定理来证明。
在三面角A-OBC中,设二面角O-AB-C为∠AB,易证∠AB=90°
由三面角余弦定理得
cos∠OAC=cos∠OAB*cos∠CAB+sin∠OAB*sin∠CAB*cos∠AB
即cosθ=cosθ1*cosθ2+sinθ1*sinθ2*cos90°=cosθ1*cosθ2