p级数等于1时为什么收敛

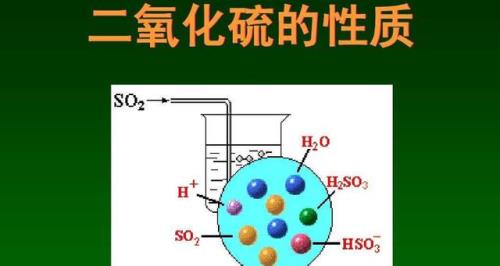
当p>1时收敛，当P≤1时发散。p级数，又称超调和级数，是指数学中一种特殊的正项级数。当p=1时，p级数退化为调和级数。p级数是重要的正项级数，它能用来判断其它正项级数敛散性。黎曼函数和黎曼猜想有关。而黎曼猜想是数学上还未解决的一个重要的猜想，其猜想是非平凡的零点的分布都位于复平面上 Re（s）=1/2 的直线上。

p级数等于1时为什么收敛

首先作为交错级数，先不看（-1）^n，1/n^p-1，极限为0，且单调减少，则交错级数收敛，整体加绝对值，由p级数1/n^p，在p>1时收敛，p≤1时发散，那么对于1/n^p-1，p>1时，p-1>0，则在p-1∈（0，1]上，加绝对值之后该级数发散，既然不严格收敛，那么可以说，原级数是条件收敛的。