史密斯正交公式是求欧式空间正交基的一种方法。
首先,我们以三个向量为例,要先进行正交化。
其次,对已经选取的向量进行正交化。
最后,对已经做完正交化之后的向量进行单位化,和以前求单位向量的方式类似,然后再对向量单位化。
史密斯正交公式的空间几何要从二维空间开始,假设肯定a1和a2两个向量对其进行正交化,当向量个数为3时,对应三维空间的几何为需要正交的原始基是正交的。
也可以推广到三维以上的欧式空间,即史密斯正交公式。
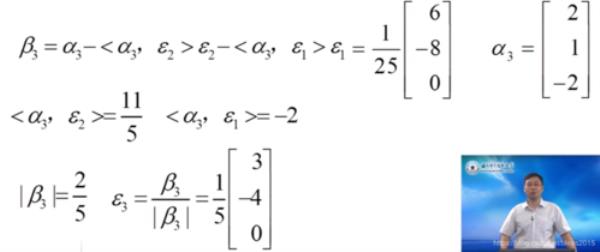
原创 | 2023-01-01 18:11:46 |浏览:1.6万
史密斯正交公式是求欧式空间正交基的一种方法。
首先,我们以三个向量为例,要先进行正交化。
其次,对已经选取的向量进行正交化。
最后,对已经做完正交化之后的向量进行单位化,和以前求单位向量的方式类似,然后再对向量单位化。
史密斯正交公式的空间几何要从二维空间开始,假设肯定a1和a2两个向量对其进行正交化,当向量个数为3时,对应三维空间的几何为需要正交的原始基是正交的。
也可以推广到三维以上的欧式空间,即史密斯正交公式。





Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com