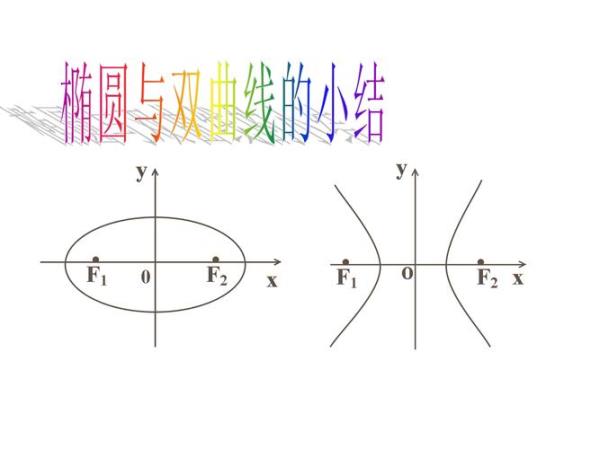
代数解法:
设等轴双曲线x^2/a^2-y^2/a^2=1
即x^2-y^2=a^2①
焦点F1(√2a,0) F2(-√2a,0)
设M(x,y)
一点M到坐标原点的距离为2
即√(x^2+y^2)=2
x^2+y^2=4②
①+②得2x^2=a^2+4
点M到两焦点的距离之积
为√[(x+√2a)^2+y^2]*√[(x-√2a)^2+y^2]
=√[(x^2+y^2+2√2ax+2a^2]*√[(x^2+y^2-2√2ax+2a^2]
=√(4+2a^2+2√2ax)*√(4+2a^2-2√2ax)
=√[(4+2a^2)^2-8a^2x^2]
=√[(4+2a^2)^2-4a^2(a^2+4)]
=√16
=4
几何解法:
设等轴双曲线x^2/a^2-y^2/a^2=1
焦点F1(√2a,0) F2(-√2a,0)
记|MF1|=m |MF2|=n ∠MOF1=θ
ΔMF1O中 由余弦定理
|MO|^2+|F10|^2-2*|MO|*|F10|*cosθ=|MF1|^2
即4+|F10|^2-4*|F10|*cosθ=m^2①
ΔMF2O中 由余弦定理
|MO|^2+|MF2|^2-2*|MO|*|MF1|*cos(π-θ)=|F20|^2
即4+|F20|^2+4*|F20|*cosθ=n^2②
由O是F1F2中点
则|F10|=|F20|=√2a
①+②得m^2+n^2=8+4a^2
由双曲线定义|m-n|=2a
m^2+n^2-2mn=4a^2
8+4a^2-2mn=4a^2
mn=4