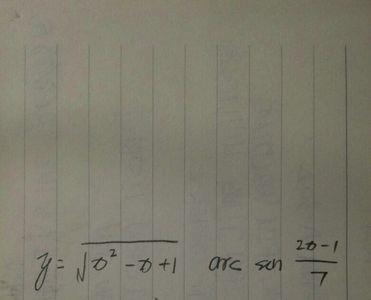sin为什么可以等于2

这是不可能的。

稍有数学常识的人都知道，锐角三角形的三角函数是在直角三角形中定义的。

在直角三角形ABC中，∠C=90゜

∠A的正弦

=∠A的对边/斜边

=b/c

因为直角三角形的直角边<斜边，即b<c，所以b/c<1

因此sinA<1，特别地A=90゜，sinA=1，从而sinA≤1。

因此，正弦值不可能大于1。

进入高中将角推广到任意角以后，正弦函数的定义域R，值域[-1，1]

也说明正弦值不可能大于1，所以你的说法是错的。

sin为什么可以等于2

sinx不会等于2。正弦函数的性质有，1，周期性，2，有界性。它是介在正1和负1之间。即丨sinx｜≤1。所以，它的函数值不可能等于0。